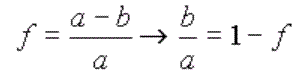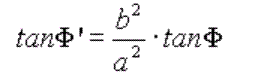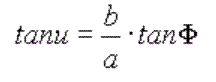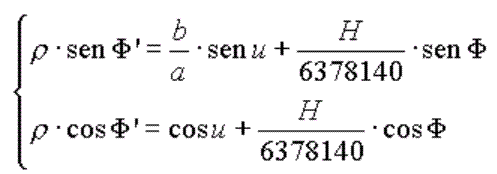Cálculo de las Efemérides
de un eclipse de Sol.
Eclipse
de 3 de octubre de 2005
Por Joaquín
García Ferrer
Explicar el cálculo de las efemérides
de un eclipse de Sol para una revista de divulgación es una cuestión
difícil. Si lo explicas superficialmente decepcionas al que espera ver
el cálculo. Si lo haces bien te alejas de la divulgación y sólo
interesa al astrónomo que ya sabe hacerlo. El astrónomo francés
Camille Flammarion del siglo XIX, cuanta una anécdota en la que tirano
que gobernaba Siracusa ordenó a Arquímedes que le evitara los símbolos
matemáticos en la lección de Astronomía, "continuemos,
que en estas cuestiones no hay privilegio para reyes" replicó Arquímedes.
En el prólogo de libro "Historia del tiempo" de Stephen Hawking
éste dice que por cada fórmula que aparece en el libro los lectores
disminuirán a la mitad. A pesar de ello decide poner una fórmula.
En el caso que nos ocupa nos vamos a ahogar en un mar de fórmulas. Ante
la dificultad he decidido hacerlo en tres etapas que son aproximaciones sucesivas
al problema, para que cada lector se quede allí donde le interese. En una
primera fase se calculan las características generales del eclipse solar,
sin entrar en el cálculo de las circunstancias locales. En una segunda
se hace el cálculo del eclipse para la localidad de Gandía, por
un método que no usa los elementos besselianos, apoyándonos en programas
(applets de Java) hechos también por mi, que están en Internet y
que son los que realmente hacen los cálculos. De esta manera lo que destaca
es el método. Quien quiera profundizar tiene para cada applet una explicación.
En una tercera fase se usan los elementos besselianos para calcular no sólo
las características locales sino la banda de anularidad, limites norte
y sur del eclipse parcial, etc. Para hacer esta parte menos pesada se usa una
hoja Excel hecha por el autor, que es la que verdaderamente hace los cálculos.
Se acaba con un applet hecho por el autor, que está en Internet y que calcula
las circunstancias locales basándose en los elementos besselianos con sólo
poner la localización.
Preliminares
Hay Eclipse de Sol cuando la sombra de la Luna cae sobre determinados lugares
de la Tierra o la Tierra entra en la zona de penumbra causada por la Luna.
El Eclipse de Sol ocurre siempre en la Luna Nueva (Sol y Luna en Conjunción)
En un eclipse de Sol, los centros de los tres astros están alineados o
casi alineados, estando la Luna entre el Sol y la Tierra.
Si la órbita
de la Luna estuviese sobre la Eclíptica (plano de la órbita de la
Tierra) , a cada revolución lunar daría lugar a un eclipse de Sol
durante el Novilunio y a un eclipse de Luna durante el Plenilunio al cabo de unos
15 días. En realidad el plano de la órbita lunar está inclinado
respecto a la eclíptica un ángulo de 5°08'13", lo que motiva,
las más de las veces, que la Luna pase por encima o por debajo del Sol
o por arriba o debajo del cono de sombra de la Tierra sin que tenga lugar el eclipse.
Solo habrá eclipses en las sicigias (palabra que engloba las conjunciones
y oposiciones del Sol y la Luna) cuando el Sol esté cerca de los Nodos
de la Luna o puntos en que la órbita lunar corta a la Eclíptica.
Este nombre proviene de que los eclipses siempre ocurren en la proximidad a dicho
plano.
Fase 1: Cálculo simplificado de las características
de un eclipse solar
Sin demasiado cálculo es posible obtener
una idea bastante precisa de las características de un eclipse de Sol o
de Luna. Para el eclipse solar la situación se complica porque para distintos
observadores en la superficie de la Tierra las circunstancias del eclipse solar
son diferentes, mientras todos los observadores de un eclipse lunar ven las mismas
circunstancias en el mismo instante.
Por esta razón no calcularemos
en principio las circunstancias locales para las que hay que usar los elementos
besselianos del eclipse y/o hacer una larga serie de cálculos.
1.
Cálculo del instante de la fase media de la Luna Nueva
Para tener
una idea del eclipse de Sol hay que calcular el instante (fecha juliana) en el
que ocurre la fase media de la Luna nueva, que afectada de aberración solar
es:
JD= 24152415020,75933 +29,53058868 k+0,0001178 T2-0,000000155 T3+
+0,0033 sen(166º,56+132º,87 T-0º,009173 T2)
--Partiendo de
una fecha donde había luna nueva JD=2415020,75933 hay que sumar k veces
el periodo sinódico lunar que es de 29,53058868 días. Un valor aproximado
de k es:
K=(año-1900)x12,3685. Para el eclipse que nos ocupa el 3 de
Octubre de 2005 tenemos año=2005,75616 así k=1308,04 por lo que
k=1308.
-- T es el tiempo en siglos julianos (36525 días cada siglo)
contado desde 0,5 de enero de 1900. Puede calcularse con bastante exactitud mediante
: T=k/1236,85). Para el eclipse del 3 de octubre de 2005 T=1,057525
-- Para
estos valores de K y T la fórmula da para la fase media de la luna nueva
el instante: JD=2453646,76919166
2. Anomalía media del Sol en
el instante
M=359º,2242+29º,10535608k-0.0000333T2-0,00000347T3
Para el instante de la luna nueva M=38429º,02991=269º,0299113
3.
Anomalía media de la Luna
M'=306,0253+385,81691806k+0,0107603 T2+0,00001236
T3
Es decir M'=504954,5662= 234,566171
4. Argumento de latitud de
la Luna
F=21.2964+390.67050646k-0.0016528T2-0.00000239T3
F=511018,317=178,3169984
El valor de F da información acerca de si ocurre un eclipse lunar o solar.
Un valor que difiere de 0º o 180º menos de 13º,9 nos dice que hay
un eclipse. Si la diferencia es mayor que 21º,0 nos dice que no hay eclipse.
Entre ambos valores el caso debe ser examinado con mas profundidad. Tras cada
lunación F aumenta en 30º,6705. Si F esta cerca de 0º el eclipse
ocurre cerca del nodo ascendente de la Luna. Si está cerca de 180º
el eclipse ocurre cerca del nodo descendente de la órbita lunar.
5.
Para obtener el instante máximo del eclipse hay que hacer unas correcciones
al tiempo de la conjunción media donde los coeficientes se dan en décimas
de día:
| Corrección |
Valor |
|
+(0,1734-0,000393T)sen M | -0,172959599 |
| +0,0021 sen(2M) |
0,000071098 |
|
-0,4068 sen (M') | 0,331454794 |
| +0,0161 sen(2M') |
0,015210701 |
|
-0,0051sen(M+M') | -0,003026717 |
| -0,0074sen(M-M') |
-0,004187546 |
|
-0,0104sen(2F) | 0,000610626 |
| Total |
0,167173358 |
--- El máximo del eclipse ocurre a JD=2453646,76919166+0,167173358=2453646,936365
--- Es decir a las 10,47276 horas=10h 28m 22s del 3 de octubre de 2005
6. Ahora calculamos S
| Término | Valor |
| +5,19595 | 5,19595 |
| -0,0048 cos (M) | 0,0000813 |
| +0.0020 cos (2M) | -0,0019989 |
| -0,3283cos M' | 0,19033598 |
| -0,0060cos(M+M') | 0,00482912 |
| +0,0041cos(M-M') | 0,00338039 |
| Total (S) | 5,39257790 |
7. Calculamos C
| Término | Valor |
| +0,2070 senM | -0,206970331 |
| +0,0024sen(2M) | 0,000081254 |
| -0,0390*sen(M') | 0,03177664 |
| +0,0115sen(2M') | 0,010864787 |
| -0,073sen(M+M') | -0,00433236 |
| -0,067sen(M-M') | -0,003791427 |
| +0,0117sen(2F) | -0,000686954 |
| Total (C) | -0,173058391 |
8. Cálculo de Gamma: Mínima distancia
del eje de la sombra lunar al centro de la Tierra
Gamma=S sen (F)+C cos(F)=
0,331362103
Gamma representa la mínima distancia del eje de la sombra
lunar al centro de la Tierra, en unidades de radio ecuatorial de la Tierra. Si
la cantidad es positiva el eje de la sombra pasa al norte del centro de la Tierra.
Si es negativa al sur. Cuando está, como es el caso entre +0.9972 y -0,9972
el eclipse solar es central, hay una línea sobre la superficie de la Tierra
donde el eclipse es total o anular.
9. Cálculo de u: Radio del
cono de la sombra lunar
El plano fundamental es el plano que pasando por
el centro de la Tierra es perpendicular al eje del cono de sombra de la Luna.
La cantidad u es el radio del cono de sombra lunar en el plano fundamental, medido
en unidades de radio ecuatorial. El radio del cono de penumbra lunar es u+0,5460.
La cantidad u se calcula:
| Término | Valor |
| +0,0059 | 0,0059 |
| +0,0046cos(M) | -0,000078 |
| -0,0182cos(M') | 0,010551675 |
| +0,0004 cos(2M') | -0,0001311 |
| -0,0005cos(M+M') | 0,000402427 |
| Total (u) | 0,016645121 |
10. Tipo de eclipse:
--Cuando gamma está, como es
el caso entre +0.9972 y -0,9972 el eclipse solar es central, hay una línea
sobre la superficie de la Tierra donde el eclipse es total o anular.
--Cuando
abs(gamma) está, 0,9972 y 1,0260 una parte del cono de sombra lunar toca
la superficie terrestre, sobre todo en las regiones polares, pero el eje del cono
de sombra no toca la Tierra, son un caso raro de eclipses anulares o totales no
centrales.
-- Cuando abs(gamma) está, 0,9972 y 1,5432+u el eclipse
es no central y en muchos de los casos es sólo parcial.
-- Cuando
abs(gamma) es mayor que 1,5432+u no hay eclipse.
-- Cuando el eclipse es central
el tipo de eclipse puede determinarse por las reglas:
++ Si u<0 eclipse
total
++ Si u>0,0047 eclipse anular (este es el caso del eclipse que nos
ocupa)
++ Si u>0 pero u<0,0047 el eclipse es anular o anular-total
Fase 2: Calculando el eclipse solar mediante applets de
Java
Pretendemos ahora calcular el eclipse para un lugar concreto,
por ejemplo Gandía, y lo haremos sin usar los elementos besselianos . Como
los cálculos son largos y complicados, usaremos applets de Java que nos
ayudaran. Debes localizar mi página http://www.geocities.com/xgarciaf/java/astrojav.htm
Cada uno de los programas usados tiene una explicación que puedes
usar si deseas más detalles.
Calcular un eclipse solar requiere calcular
lo mejor posible las posiciones del Sol y de la Luna y sus movimientos horarios.
Para ello:
1. Cálculo de la posición del Sol:
Utiliza
de Efemérides la opción 1 (http://www.geocities.com/xgarciaf/java/geosol2.htm
)
Vamos a calcular la posición del Sol el 3 de Octubre de 2005 a las
8h 0m 0s de T.U. tras llenar los datos y darle al botón Calcular aparecen
los resultados Longitud solar=190º,178869
Distancia Sol-Tierra=1,00054
U.A. En el cálculo se tiene presente que la órbita de la Tierra
es una elipse y que se cumple la ley de las áreas, aplicando la ecuación
de Kepler.
El cálculo de la distancia de la Tierra al Sol permite calcular
en ese instante el radio angular del Sol. A la distancia de 1 Unidad Astronómica
es de 16' 1"=16,0166'. Para calcular el tamaño
a la distancia
real hay que dividir por la distancia puesto que cuanto más lejos está,
se ve de menor tamaño radio solar=16,0166/1,00054=16,0008'
El semidiámetro
aparente del Sol es 16'1", variando desde 15' 45" a 16' 17" en
el transcurso de un año, por ser la órbita de la Tierra alrededor
del Sol elíptica.
Mientras que el semidiámetro lunar es de 15'
32" variando por idéntica razón entre 14' 43" y 16'26"
durante un mes lunar.
Sólo durante una fracción de la órbita
lunar, cuando la luna está cerca del perigeo tiene suficiente tamaño
para causar un Eclipse de Sol Total.
Apliquemos el programa una hora después:
Longitud solar=190º,219887 así que el Movimiento horario del Sol=0,04102
º/h
2. Cálculo de la posición de la Luna
Utiliza
de Efemérides la opción 5 (http://www.geocities.com/xgarciaf/java/poslun.htm
). Vamos a calcular la posición de la Luna el 3 de Octubre de 2005 a las
8h 0m 0s de T.U. Hacer dicho cálculo con exactitud es muy complicado porque
la Luna además de estar sometida a la atracción de la Tierra es
perturbada de una forma apreciable por la acción del Sol. Este cálculo
se efectúa para un observador situado en el centro de la Tierra. El cálculo
da:
| Coordenadas
eclípticas | Coordenadas ecuatoriales |
| Longitud lunar=189º,02888 | Ascensión Recta=12h
33m 50,7 s |
| Latitud lunar=0º,4228086 | Declinación
=-3º11'24,57" |
Las coordenadas eclípticas
fijan la posición de un astro atendiendo al plano de la eclíptica
que es por donde se desplaza la Tierra. La latitud de la Luna no es muy grande
porque si no la Luna pasaría por arriba o debajo del Sol y no taparía
al Sol. Las coordenadas ecuatoriales tienen como referencia al ecuador y los meridianos
celestes. La declinación es similar a la latitud y es el ángulo
que forma el astro con el ecuador. La ascensión recta es similar a la longitud
y es un ángulo donde 1 hora=15º. El "Greenwich celeste"
es el punto Aries.
En la misma pantalla obtenemos el radio lunar que es de
15,06894'. Está claro que esta vez la Luna no tapa al Sol y el eclipse
es anular.
El semidiámetro lunar es de 15' 32" variando por razón
de que la órbita es elíptica entre 14' 43" y 16'26" durante
un mes lunar.
Sólo durante una fracción de la órbita
lunar, cuando la luna está cerca del perigeo tiene suficiente tamaño
para causar un Eclipse de Sol Total.
El paralaje lunar es una medida de
la distancia de la Luna y es el ángulo que desde el centro de la Luna abarca
el radio ecuatorial de la Tierra. Para ese día y hora vale 55,3011348'=55'18".
El paralaje solar es 400 veces menor porque el Sol está 400 veces más
lejos, el semidiámetro de ambos astros es similar porque el Sol es 400
veces más grande que la Luna. El Eclipse Total de Sol existe por una extraordinaria
coincidencia. Los discos del Sol y la Luna, vistos desde la Tierra son casi iguales;
uno y otro apenas excenden el medio grado. Estando el Sol 400 veces más
lejos que la Luna es 400 veces más grande.
Si en la misma pantalla
cambiamos la hora y ponemos las 9h de T.U.:
| Coordenadas eclípticas | Coordenadas ecuatoriales |
| Longitud lunar=189º,545367 | Ascensión Recta=12h 35m
40,4 s |
| Latitud lunar=0º,375172 | Declinación
=-3º26'13,34" |
Paralaje lunar=55,3190'=0º55'19,14"
3.
Corrección de la posición de la Luna por paralaje
La distancia
lunar es sólo de unos 60 radios lunares por lo que un cambio en la posición
del observador sobre la Tierra tiene influencia en la posición de la Luna,
tal como la ve el observador y por tanto en su observación del eclipse.
La posición lunar se ha calculado para un observador situado en el centro
de la Tierra. Ahora vamos a calcular las posiciones de la Luna para un observador
situado en Gandía Latitud =38º 58' Longitud =0º 11' W. Lo haremos
usando un applet java del menú Coordenadas y Tiempo: Conversión
de coordenadas. La opción 10. Corrección por paralaje diurno de
las coordenadas ecuatoriales (http://www.geocities.com/xgarciaf/java/paralaje.htm
) permite saber a las 8horas 0m de T.U. la posición lunar, vista desde
Gandía:
Repitiendo el cálculo para las 9h 0m 0s tenemos para
las coordenadas lunares en Gandía:
| Coordenadas ecuatoriales Luna a 8h 0m | Coordenadas ecuatoriales Luna
a 9h 0m |
| AR=12h 36m 15,55s | AR=12h 37m 36,8s |
| Dec= -3º46'39" | Dec= -4º2'59,4" |
4. Conversión a eclípticas de la posición
lunar
Mediante la opción 1 Conversión de Ecuatoriales a
Eclípticas (http://www.geocities.com/xgarciaf/java/trasfor1.htm
)se pueden calcular las coordenadas eclípticas en ese mismo instante:
| Coordenadas eclípticas Luna a 8h 0m | Coordenadas
eclípticas Luna a 9h 0m |
| Longitud=189º,819032=189º49'8,5" | Longitud=190º,231143=190º13'52,1" |
| Latitud= -0º,105921= -0º6'21,3" | Latitud=
+0º,0007447= +0º0'2,7" |
5. Movimiento horario
de la Luna
Ahora ya no necesitamos ningún applet para terminar
los cálculos:
En una hora la luna ha cambiado su posición en:
Longitud: Long=190,231143-189,81903256=0,41211 º/h
Latitud: : Lat=0,0007447-0,105921=-0,105176º/h
6.
Instante del máximo del eclipse en Gandía:
Para el Sol deberíamos
hacer la misma corrección por paralaje, pero el efecto es tan pequeño
que lo vamos a obviar. A las 8h 0m 0s de T.U. la diferencia entre las longitudes
de la Luna y del Sol es:
Longitud lunar- Longitud solar =189,819032-190,178869=-0º,35983
Pero la Luna viaja por término medio unas 12 veces más rápido
que el Sol.
La velocidad neta de la Luna respecto al Sol es: 0,41211-0,04102=0,37109º/h
La diferencia en longitudes se compensa en 0,35983/0,37109=0,969657=58m 11s
El instante del máximo del eclipse en Gandía es 8h 58m 11 s de T.U.=8h59m
19s de T.E.
En ese momento la Longitud solar es 190,178869+0,04102x0,969657=190º,2186
Sabemos que un cálculo más preciso, considerando los elementos besselianos
da para el máximo 9h 2m 2,3s de T.U. Un error de algo más de 3 minutos.
Sabemos que ese día la hora oficial irá dos horas adelantada serán
las 11h 2m 2,3s
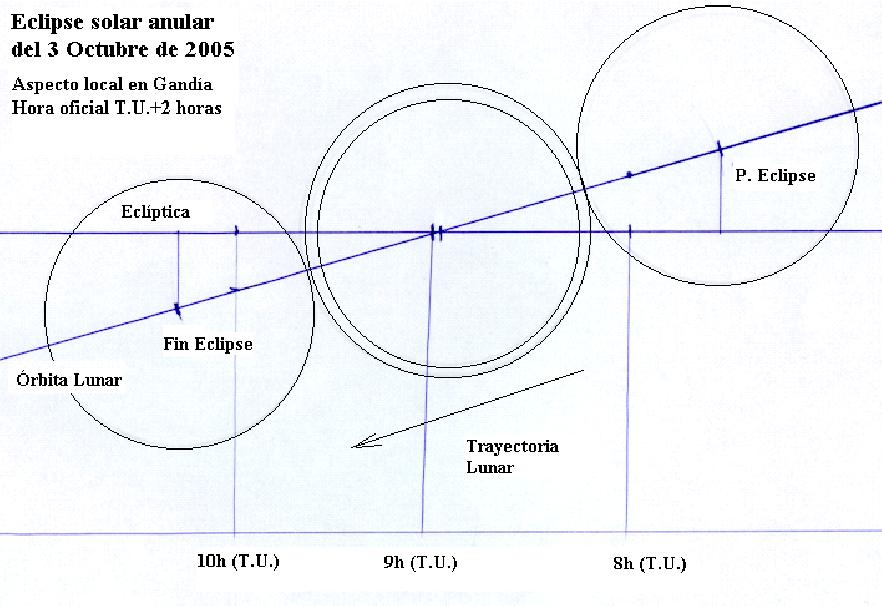
7. Dibujo del aspecto del eclipse en Gandía:
Dibujemos una línea horizontal que representa la eclíptica y otra
paralela que representa el tiempo. Elijamos como escala para 1 hora 4 cm. Coloquemos
tres marcas temporales, la de las 9h T.U. hacia el centro del diagrama y las otras
dos a 4 cm.
El movimiento relativo Luna- Sol es 0,37109 º/h por lo que
1º representa a esta escala 4/0,37109=10,78cm.
El radio solar es 16,0008'=0,2668º
que corresponden a 2,87cm. A las 8h 58m11s tracemos el círculo solar.
Tracemos la posición de la Luna a las 8h. Su latitud es 0º,10592 que
representa 1,14cm por encima de la eclíptica.
Tracemos la posición
de la Luna a las 10h. El movimiento en latitud es -0,105176º/h así
que la latitud a las 11h es Lat=0,10592-0,105176x2= -0º,105176 lo que representa
1,12 cm por debajo de la eclíptica. Si unimos los dos puntos tendremos
la trayectoria lunar. Esta trayectoria cruza la eclíptica por la línea
de tiempo de las 8h 58m 11s
El radio lunar es 15,0689'=0,25115º a esta
escala 2,707 cm. Tracemos el círculo lunar que queda inmerso en el solar
dejando una corona característica del eclipse anular.
Si sobre la trayectoria
lunar, partiendo del limbo solar tomamos el radio lunar llegamos a los puntos
PE= Principio del eclipse parcial y FE= Final del eclipse parcial. Estos ocurren
gráficamente 18mm antes de las 8h es decir a las 7h 33m y a 12mm después
de las 10h es decir a las 10h 18m de T.U: El horario real es 7h 42m y 10h 29m.
No podemos esperar más de un dibujo. Mejoraremos el resultado en la fase
3
8. Cercanía del Sol y Luna al Nodo descendente
La órbita
de la Luna está inclinada 5º 8' respecto a la Eclíptica, a
la que corta en dos puntos llamados Nodo ascendente y descendente. Si los Nodos
estuviesen fijos el Sol los atravesaría cada medio año y si coincidiese
la proximidad del paso con una sicigia, se produciría un eclipse. Los eclipses
ocurrirían siempre en las mismas constelaciones zodiacales. Pero esto no
es así:
Los nodos retrogradan sobre la Eclíptica, dando una
vuelta en 18,6 años
La longitud media del Nodo ascendente es:
N=151º,950429-0º,529539
(J-2444238,5)
Para el 3 de octubre de 2005 la fecha juliana J=2453646,876
la longitud nodo ascendente es 13º,74. Como la anomalía media solar
es M=269,0229 y la longitud del nodo es:
N'=N-0,16 sen(M)=13º,9001
El nodo descendente tiene una longitud N=180+13,9001=193,9001
Y la distancia
entre el Sol y el nodo descendente es de 3º,6816, que corresponde a un eclipse
total o anular.
Fase 3 : Cálculo usando los
elementos besselianos
Explicación de los Elementos besselianos
1. Tiempo dinámico TD y el TU
El Tiempo dinámico o tiempo
de efemérides es totalmente uniforme, mientras que el Tiempo Universal
basado en la rotación de la Tierra presenta irregularidades. La diferencia
DT=TD-TU no se conoce con antelación, en julio de 1981 era de 52 seg. Para
el 3 de octubre de 2005 se extrapola que esta diferencia será de 68 segundos.
2.
Coordenadas geográficas del lugar de observación
La Tierra
no es una esfera sino un geoide (su sección de corte por el meridiano es
una elipse) y para predecir las circunstancias locales con precisión hace
falta distinguir entre:
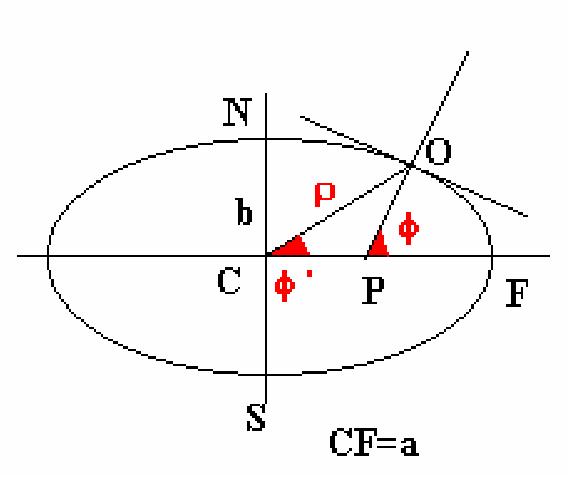

además de tener presente la altura del observatorio en metros.
C es el centro de la Tierra, N el polo Norte, CF es el radio ecuatorial y el plano
tangente que pasa por el observador O el plano del horizonte, la perpendicular
OP a dicho plano determina con el ecuador la latitud geográfica, la línea
OC que determina la distancia del observador al centro de la Tierra determina
con el ecuador la latitud geocéntrica. Ambas son iguales en los polos y
ecuador, para todas las demás latitudes:
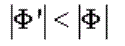
Sea f el achatamiento de la Tierra. Por definición:
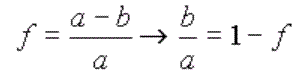
donde a es el radio ecuatorial y b el radio polar. De las mediciones de la
Tierra sabemos que: f=1/298,257 por lo que b/a=0,99664719.
Se puede demostrar
que:
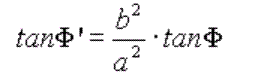
Introduciendo
la variable auxiliar u:
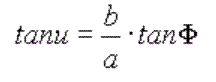
resulta que las variables necesarias 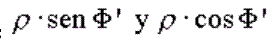 para
calcular eclipses y ocultaciones se calcula mediante:
para
calcular eclipses y ocultaciones se calcula mediante:
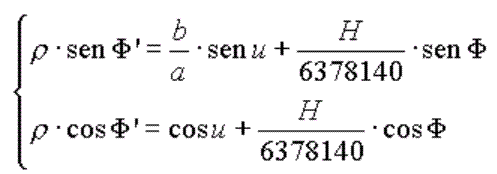
donde H es la altura del observador en metros sobre el nivel del mar.
-- Calcular las coordenadas geocéntricas de Gandía, latitud geográfica
38º 58' N y longitud 0º 11' W a una altura de 0 m.
tg u=0,99664719.
tg 38º58'=0,806109
sen u=0,627591; b/a sen u=0,6254868
cos u=0,7785433
3.
Fecha juliana de cada eclipse.
Esta fecha normalmente se expresa en TU,
pero puede expresarse en T. de Efemérides añadiendo el DT y dando
lugar al JDE=2453646,94. Este se expresa en el momento del máximo del eclipse,
es decir cuando el eje de la sobra lunar está más próximo
al centro de la Tierra.
4. Lunación K
La lunación
0 corresponde a la Luna Nueva del 6 de Enero del año 2000, así que
antes del 2000 k<0. Para el eclipse del 3 de octubre de 2005 K=71. Para obtener
el número de lunación de E.W. Brown hay que añadir 953 a
k es decir le corresponde una lunación Brown de 1024.
5. Número
Saros
Es el número de serie de un eclipse dentro de un periodo
Saros. Dos eclipses con el mismo número Saros son homólogos. Número
Saros =134 para este eclipse. Fue introducido por G.Van der Bergh. Los eclipses
con número de Saros impar tienen lugar en el nodo ascendente mientras que
si es par como es el caso, ocurren en el nodo descendente.
6. Tipo de
Eclipse
Se indica mediante una letra p= Eclipse parcial, r=anular central,
t= total central, rt= anular-total (anular en una parte del camino y total en
otra). Más raramente hay eclipses no centrales cuando una parte del cono
de sombra de la Luna toca la superficie de la Tierra, pero no su eje. Pueden ser
(r)= anular no central y (t)=total no central. Si un eclipse es parcial le acompaña
el valor 0<f<1 de la magnitud, es decir el mayor del elipse en cualquier
lugar de la Tierra. Este número se da con tres decimales. Es importante
destacar que un eclipse total o anular, se ve así sólo en una estrecha
franja de la superficie de la Tierra. Al Norte o Sur de este camino hay grandes
regiones para los cuales se ve como parcial.
7. Gamma
Es la mínima
distancia desde el eje de cono de sombra lunar al centro de la Tierra, medido
en unidades ecuatoriales. Esta distancia es positiva si el eje pasa por el Norte
del centro de la Tierra y negativa si pasa al Sur. Debido al achatamiento de la
Tierra su valor límite es 0,997. El cambio de entre dos eclipses homólogos
pertenecientes a dos periodos Saros consecutivos, es más grande si la Tierra
está cerca del afelio (Junio-Julio) y menor cuando está cerca del
perihelio (Diciembre-Enero). Para el caso que nos ocupa Gamma=0,33041. Recordemos
que en la aproximación primera obtuvimos un valor de 0,33136.
8.
Hora de referencia T0
Es la parte entera de la hora a la que ocurre al
máximo del eclipse. Esta es la hora de referencia para los elementos besselianos
del eclipse. Para el eclipse del 3 de octubre son las 11 horas. Recordemos que
para el máximo del eclipse en la aproximación inicial obtuvimos
las 10h 28m 22s
9. Elementos besselianos
-- Estos elementos
caracterizan la posición geocéntrica de la sombra de la Luna respecto
a la Tierra. Las tangentes exteriores al Sol y a la Luna determinan el cono de
sombra de la Luna. La tangentes interiores el cono de penumbra. El eje común
de los dos conos es el eje de la sombra. El plano geométrico perpendicular
al eje de sombra se llama plano fundamental. El eje X es la intersección
del plano fundamental con el Ecuador y es positivo hacia el este. El eje Y pertenece
al plano fundamental, es perpendicular al X y positivo hacia el Norte. El eje
Z es perpendicular a los anteriores, paralelo al eje de sombra y positivo hacia
la Luna. El eje de la sombra corta al plano fundamental en un punto (X,Y) medido
en unidades de radio ecuatorial de la Tierra. Las cantidades X0, Y0, son los valores
en el instante de referencia T0. Los valores en otro instante se calculan mediante
una expresión polinómica cuyos coeficientes también vienen
tabulados, por ejemplo: 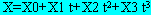 donde
t viene expresado en horas a partir de T0 y es negativo si es anterior a T0. Los
elementos X,Y se expresan por polinomios de tercer grado.
donde
t viene expresado en horas a partir de T0 y es negativo si es anterior a T0. Los
elementos X,Y se expresan por polinomios de tercer grado.
Para el eclipse
de 3 de octubre de 2005:
X0=0.365979; X1=0.4554791; X2=0.0000099; X3=-0.00000545;
Y0=0.175659; Y1=-0.2508066; Y2=0.0000075; Y3=0.00000317;
-- El eje de la
sombra apunta a un lugar de la esfera celeste con declinación d y ángulo
horario M. Las cantidades d0, M0, son los valores en el instante de referencia
T0. Los valores en otro instante se calculan mediante una expresión polinómica
de segundo y primer grado respectivamente d y M se expresan en grados y parte
decimal.
D0=-4.09224; D1=-0.01549; D2=0.000001;
M0=347.75359; M1=15.004341;
--
El radio del cono de penumbra en el plano fundamental es L1 y el del cono de sombra
es L2 y es positivo en un elipse anular y negativo en uno total. Los valores en
otro instante se calculan mediante una expresión polinómica de segundo
grado, cuyos coeficientes también vienen tabulados:
L10=0.562654; L11=-0.0001022;
L12=-0.00001;
L20=0.016448; L21=-0.0001017; L22=-0.0000103;
-- Los ángulos
f1 y f2 son los que forman el cono penumbral y de sombra con el eje de la sombra.
Las tangentes de f1 y f2 se consideran constantes durante el eclipse y son siempre
positivas.
F1=0.0046741; F2=0.0046508;
" El cálculo de los
elementos besselianos de un eclipse se hace a partir de las posiciones del Sol
y de la Luna está en la página 110 de "Les éclipses
de Soleil" y rebasa los objetivos de este artículo. En Internet hay
ficheros con dichos elementos desde el año -2800 al 3000.
Aplicación
Práctica del uso de los elementos Besselianos:
Para evitar
hacer los cálculos hay en la dirección de Internet (http://personal.telefonica.terra.es/web/xgarciaf/eclipse/eclipse.xls
), una hoja de cálculo Excel que los hace por nosotros. La primera hoja
Bessel contiene los elementos besselianos de los eclipses de Sol desde el año
1951 al 2200. El eclipse del 3 de octubre de 2005 es el que ocupa la fila 122.
--
Curva del eclipse central, para tiempos dados. (hoja esm14)
Se trata de
calcular para un tiempo dado la posición de la sombra. Para ello en la
hoja esm14 y en la celda F1 hay que colocar 122 que corresponde al eclipse del
3 de octubre de 2005: En la fila 4 aparecen ya los elementos besselianos. En C1
aparece la fecha del eclipse. También es necesario ingresar la diferencia
entre el tiempo dinámico y universal TD-TU. En este caso 68 segundos. En
D2 debe ponerse la hora (por ejemplo 9) y en E2 los minutos ( por ejemplo 2) de
la hora en que quiere calcularse la posición de la sombra. La hoja de cálculo
ya tiene todos los resultados. Así a las 9h 2m de T.U. el centro de la
mancha del eclipse anular es 38º 54' N y 0º 13'W. La duración
del eclipse anular es de 254 segundos y la anchura de la mancha es de 182,98Km.
La altura del Sol sobre el horizonte es de 32º,17 y la relación de
diámetro Luna/Sol de 0,95. Variando t y dibujando sobre un mapa círculos
del radio indicado por la mitad de la anchura y con centro en las coordenadas
calculadas en cada caso, puedes hacerte una idea de la banda central de anularidad.
Dibujando las coordenadas trazarás la línea de centralidad. Variando
el tiempo verás que hasta las 8h 43m no hay eclipse central y este se sitúa
a 48º1'N 36º 40' W (principio del eclipse anular) ¿A qué
hora y lugar acaba el eclipse central?
Para saber las fórmulas utilizadas
puede verse una explicación en la página de dirección:
(http://personal.telefonica.terra.es/web/xgarciaf/eclipse/esm14.htm)
--
Puntos extremos de la línea central. (hoja esm15)
Coloca en F1
122 para elegir el eclipse. En los renglones 24 y 25 verás la hora del
principio del eclipse anular y del final a las 12h 21m y si llevas esa hora a
esm14 te indica el lugar. Pon 12h 20m y aparece -9º 51'S 77º 26' E en
pleno Océano Indico.
Para saber las fórmulas utilizadas puede
verse una explicación en la página de dirección:
(http://personal.telefonica.terra.es/web/xgarciaf/eclipse/esm15.htm)
--
Curva de un eclipse para longitudes dadas. (hoja esm17)
Puede parecer
preferible calcular los puntos de la línea central para longitudes dadas,
en vez de hacerlo para tiempos dados. Si se eligen longitudes enteras pueden resultar
más fáciles de dibujar en un mapa. Sea L la longitud elegida. Deseamos
encontrar la correspondiente latitud y el instante TD en que el eclipse central
atraviesa esa longitud.
Para usarlo pon 122 a F1 para elegir el eclipse.
En I2 68 segundos de diferencia TD-TU.
Por ejemplo vamos a averiguar la línea
de centralidad que atraviesa España para lo que elegiremos longitudes de
9ºW y 0º
Para 9ºW en F2 ponemos 9, pues el criterio de signos
utilizado es positivo al oeste. Tras seis aproximaciones dice que el punto de
centralidad tiene una latitud 42,51027 N=42º30'37"N, lo que nos sitúa
en la desembocadura de la Ría de Arosa, cerca de Aguiño, en Galicia
a las 8h 54m 5s de TD y a las 8h 52m 57s de T.U. con una fase anular que dura
248,38s.
Para 0º el punto de centralidad tiene una latitud 38,8026 N=38º48'10"N
lo que nos sitúa cerca de Pedreguer en La Marina Alta a las 9h 3m25s TD,
9h 2m 17s de T.U. con una fase anular que dura 254,32s. Puedes averiguar para
una longitud de 5ºW si se comete mucho error al suponer recta la línea
de centralidad.
Puedes conseguir un mapa de la comarca de La Safor y dibujar
la línea de centralidad.
Dibuja la línea de centralidad de 10
en 10º de longitud desde 40ºW a 80ºE (exactamente desde 36º
40' W a 77º 26' E)
Para saber las fórmulas utilizadas puede verse
una explicación en la página de dirección:
(http://personal.telefonica.terra.es/web/xgarciaf/eclipse/esm17.htm
)
En B56 calcula la altura del Sol. Si la longitud F2 no es adecuada obtendremos
una altura del Sol negativa.
-- La bandera de D1
Las hojas
esm19,21,22,23 contienen en D1 una bandera cuyos valores y significado son:
| Hoja |
D1 | Significado |
| esm19 | 1
| Límite Norte del eclipse Central |
| | -1 |
Límite Sur del eclipse Central |
|
esm21 | 1 |
Límite Norte del eclipse Parcial |
|
| -1 | Límite
Sur del eclipse Parcial |
|
esm22 | 1 | Curva
Norte de igual magnitud |
| |
-1 | Curva Sur de igual magnitud |
| esm23 |
-1 | Primer contacto |
| | 0 |
Máximo eclipse |
| |
1 | Último contacto |
-- Cálculo del límite Norte-Sur de un eclipse total
o anular (esm19)
Para usarlo 122 a H1 para elegir el eclipse. En I2 68
segundos de diferencia TD-TU
Por ejemplo vamos a averiguar la banda de anularidad
que atraviesa España para lo que elegiremos longitudes de 9ºW y 0º
Para 9ºW en F2 ponemos 9 pues el criterio de signos utilizado es positivo
al oeste.
No olvidar poner un 1 en D1 para obtener la latitud del Límite
Norte 43,4686132=43º28'7"
Si ponemos en D1 un -1 obtenemos para
la latitud del Límite Sur 41,5598737=41º 33'35"
Para 0º
de longitud el límite norte está a una latitud de 39,7764241=39º46'35"
y el límite sur a una latitud de 37,8367761=37º50'12"
Dibuja
el Límite Norte y Sur para la Comunidad Valenciana.
Dibuja la banda
de anularidad de 10 en 10º de longitud desde 40ºW a 80ºE (exactamente
desde 36º 40' W a 77º 26' E).
Para saber las fórmulas utilizadas
puede verse una explicación en la página de dirección:
(http://personal.telefonica.terra.es/web/xgarciaf/eclipse/esm19.htm
)
-- Cálculo del límite Norte-Sur del área de visibilidad
del eclipse parcial (esm21)
Un eclipse total o anular como el del 3 de
octubre de 2005 es parcial para la mayoría de los observadores fuera de
la línea de centralidad. Vamos a calcular los límites Norte y Sur
del eclipse parcial, por el procedimiento explicado en la dirección (http://personal.telefonica.terra.es/web/xgarciaf/eclipse/esm21.htm)
Vamos a calcular el límite sur para una longitud de 0º, para ello
en la hoja esm21 ponemos en H1 122 para elegir el eclipse, en I2 68 segundos de
diferencia TD-TU, en F2 para la longitud 0 y la bandera D1 con -1 obtenemos una
latitud -3,54460347=3º 32'40"S. Para calcular el límite norte
a esta misma longitud hay que poner en D1 un 1 obtenemos un valor absurdo.
Debe observarse que muchos eclipses sólo tienen un límite para la
zona de parcialidad. El otro límite debe reemplazarse por la curva Sol
en el horizonte.
Incluso si los dos límites existen puede haber problemas
si alguno de ellos se acerca a las regiones polares. Para unas longitudes la curva
no existe, mientras para otras parece no existir si se calcula por el procedimiento
descrito, aunque realmente sí existe lo que ocurre es que la curva esta
más allá del polo Norte o Sur y por tanto se sitúa a una
longitud que realmente difiere 180º de la considerada. No obstante puede
obtenerse si la iteración comienza para una latitud de 80º si está;
cerca del P. Norte o -80º si está cerca del Sur en vez de empezar
la iteración a 0º de latitud.
Si en vez de 0º de longitud
ponemos 180º obtenemos el límite norte a una latitud 82,2276699 N.
Dibuja el límite sur del área de parcialidad de 10 en 10º de
longitud desde 40ºW a 80ºE (exactamente desde 36º 40' W a 77º
26' E).
Dibuja el límite norte del área de parcialidad de 10
en 10º de longitud desde 40ºW a 80ºE (exactamente desde 36º
40' W a 77º 26' E) ten presente que para longitudes entre 36 W y 0 E hay
que poner las diametralmente opuestas. Para 10ºE hay que poner 170W y empezar
la iteración en 80 (B8). Para 20,30 y 40ºE no hay límite norte.
--
Curvas de igual magnitud para un eclipse parcial (esm22)
La determinación
de las curvas norte y sur para una determinada magnitud G, inferior a la fase
máxima, puede lograrse mediante un procedimiento similar al enunciado en
el apartado anterior. Como el eclipse de 3 de Octubre de 2005 es anular vale cualquier
fase.
Por ejemplo, trazar las curvas norte y sur de los lugares con fase 0,8
a las longitudes de la Península Ibérica entre 10W y 5E
Para
0ºW de longitud. Para usarlo pon 122 en H1 de la hoja esm22 para elegir el
eclipse, en I2 68 segundos de diferencia TD-TU, en F2 la longitud 0, en D1 1 para
la curva norte y en F1 la magnitud 0,8 la latitud calculada es 45,7760169 por
arriba de Burdeos en Francia y por el sur, D1 con -1 y resulta una latitud 31,8575721
en el Atlas argelino. Toda la península tendrá una magnitud mayor
que 0,8.
Para saber las fórmulas utilizadas puede verse una explicación
en la página de dirección:
(http://personal.telefonica.terra.es/web/xgarciaf/eclipse/esm22.htm
)
-- Circunstancias locales (esm23)
Vamos a determinar ahora
con mayor exactitud las circunstancias locales para Gandía. Para usarlo
122 en H1 de la hoja esm23 para elegir el eclipse, en I2 68 segundos de diferencia
TD-TU. La latitud de Gandía es 38º 58'=38,9666 se debe colocar en
B6, la longitud 0º 11' W=+0,18333 en D6 y altura 0 metros en F6.
Primer
contacto: En D1 poner -1 Eclipse parcial empieza a las 7h 43m 16s TD es decir
a las 7h 42m 8s de T.U. y por tanto 9h 42m 8s hora oficial con el Sol a una altura
Sol de 18º,7. Angulo P= 308,338 (sentido antihorario)
Máximo del
eclipse: En D1 poner 0. Eclipse anular en su máximo a las 9h 3m8s TD es
decir 9h 2m 0s TU y por tanto 11h 2m 0s., con el Sol a una altura de 32º,17
y un Angulo P= 220º,631 (sentido antihorario). La magnitud máxima
del eclipse es 0,974896293 porque la Luna con diámetro 0,9536 veces el
del Sol no lo tapa completamente.
Último contacto: En D1 poner +1 Eclipse
parcial termina a las 10h 30m 58s TD es decir a las 10h 29m 50s de T.U. y por
tanto 12h 29m 50s hora oficial, con el Sol a una altura de 43º,16. Angulo
P= 132,643 (sentido antihorario).
Para saber las fórmulas utilizadas
puede verse una explicación en la página de dirección:
(http://personal.telefonica.terra.es/web/xgarciaf/eclipse/esm23.htm
)
-- Dibujo del eclipse en Gandía
Ahora puedes dibujar
el eclipse tal como se verá en Gandía. Traza el contorno del Sol
a cualquier tamaño y contando el ángulo P= 308,338 (sentido antihorario)
encontrar el centro de la Luna, contando, a partir del borde del Sol el radio
de la Luna. Traza el círculo de la Luna al principio del eclipse. Análogamente
para el final. Uniendo los centros de la Luna del principio y final y cortando
con el ángulo P del máximo tendremos el centro lunar en el máximo.
Trazar el círculo lunar en el máximo. Compara con el dibujo hecho
en la aproximación segunda. Para ello traza el radio solar del mismo tamaño.
Para ver un aspecto del dibujo acceder al mismo dibujo para la ciudad de Valencia:
(http://personal.telefonica.terra.es/web/xgarciaf/es2005/031005_cirloc.jpg
)
Applet de Java que calcula las circunstancias locales
En la dirección (http://personal.telefonica.terra.es/web/xgarciaf/es2005/cirloc.htm
) hay un applet que calcula las circunstancias locales con sólo poner la
latitud, longitud y altura del lugar. Hay unas instrucciones de uso que reproducimos:
Instrucciones
para el uso del Applet Eclipse de 3 de Octubre de 2005
-- Para
la banda de Anularidad, no se contempla el cálculo del principio y fin
del eclipse Anular (contactos interiores de la Luna con el Sol). Teniendo presente
que el eclipse anular dura unos 4 minutos, a muy grosso modo empieza 2 minutos
antes del máximo y acaba 2 minutos después del máximo. En
la tabla donde hay ciudades de España si se contemplan estos tiempos.
-- El tiempo para los que se calcula un eclipse o cualquier fenómeno astronómico
es el tiempo dinámico de la física que fluye uniforme. No obstante
la vida social está regida por el Tiempo Universal (T.U.) que está
ligado a la rotación de la Tierra y por tanto no es uniforme. Es imposible
saber con antelación cual es la diferencia entre ambos tiempos DT=TD-TU
pero un ajuste lo sitúa para esta fecha en 68,33 segundos. Si la previsión
no se cumpliese el TU habría que retocarlo en la cantidad que discrepase
de ese valor. La hora oficial española es TU+2 así que habrá
que añadir dos horas para saber a qué hora ocurre el eclipse.
-- Para la previsión local que hace este applet hay que colocar la latitud
y la longitud en º ' y ".
++ Si la desconoces debes usar un mapa
que tenga dibujados los meridianos y paralelos para averiguar dichos valores.
++ En España la latitud es Norte, sólo si quieres saber las circunstancias
locales de un lugar del Hemisferio Sur debes pulsar en el cuadro S. La Península
se extiende desde 36º a los 44º
++ La longitud de la mayoría
de los lugares de España está el Oeste del meridiano de Greenwich,
sólo si está al este (partes de la C. Valenciana y Aragón,
Cataluña y las Islas Baleares tienen longitud este y debes pulsar en el
cuadro E. La longitud se extiende desde 10ºW a 5ºE.
++ Debes llenar
los º ' y " . Si desconoces los segundos pon 0. Análogamente
debes poner la altura sobre el nivel del mar en metros. Si la desconoces pon 0.
++ La latitud va desde 0 a 90. La longitud va desde 0 a 180. Debes colocar un
valor que indique un lugar sobre la superficie de la Tierra, es decir con valores
posibles.
++ 1º son 60' y 1' son 60" por lo que los campos minutos
y segundos no pueden superar el valor 59.
-- Este eclipse es Anular porque
la Luna está más alejada de lo normal y no llega a cubrir completamente
el Sol. La relación de diámetros indica que la Luna cubre el 95%
del diámetro del Sol. Este dato se calcula en el instante del máximo
del eclipse.
-- Si para una localidad (no de España en este eclipse)
una fase del eclipse ocurre cuando la altura del Sol sobre el horizonte es negativa,
significa que esa parte del eclipse no es visible desde ese lugar.
-- El ángulo
P es el ángulo de posición del centro de la Luna contado desde el
N del Sol y hacia el Este. Se facilitan al principio y final del eclipse parcial,
los contactos exteriores y también durante el máximo del eclipse.
Bibliografía
** Elements
of solar eclipses 1951-2200. Jean Meeus. Willmann Bell
** Astronomical Formulae
for calculators Jean Meeus. Willmann Bell
** Practical astronomy with your
calculator Peter Duffett-Smith. Cambridge University Press
** Les Éclipses
de Soleil. Institut de mécanique céleste. EDP Sciences
** Applets
de Java para Astronomía http://www.geocities.com/xgarciaf/java/astrojav.htm
** Hoja de cálculo Excel: http://personal.telefonica.terra.es/web/xgarciaf/eclipse/eclipse.xls
** La página http://www.telefonica.net/web/xgarciaf/es2005/031005es.htm
del eclipse del 3 de octubre de 2005: hay información sobre la trayectoria
etc. destacando efemérides para las ciudades españolas y para todos
los pueblos de la C. Valenciana que están dentro de la banda de anularidad.
(Nota: Está página y el applet Applet de Java que calcula las circunstancias
locales está recomendado en Enlaces de interés en el tríptico
que sobre el acontecimiento publican el Instituto de Astrofísica de Canarias
y el Ministerio de Educación y Ciencia.